Study the outbreak and end characteristics of epidemic and social transmission from the perspective of data

Nana Zhang^1*,Shuhaida Md. Noor¹,Wenxu Yang²

¹ School of Communication, University Sains Malaysia, Pulau Pinang, Malaysia

² School of Civil Engineering, University Sains Malaysia, Pulau Pinang, Malaysia

*Corresponding Author:

Nana Zhang
School of Communication, University Sains Malaysia, Pulau Pinang, Malaysia
E-mail: zhangnana@student.usm.my

Citation: Zhang N, Noor s, Yang W (2022) Utilizing Virtual Reality and Three- Dimensional Space, Visual Space Design for Digital Media Art. Global Media Journal, 20:57.

Received: 17-Oct-2022, Manuscript No. gmj-22-79708; Editor assigned: 19-Oct-2022, Preqc No. gmj-22-79708; Reviewed: 02-Nov-2022, QC No. gmj-22-79708; Revised: 07-Nov-2022, Manuscript No. gmj-22-79708 (R); Published: 14-Nov-2022, DOI: 10.36648/1550-7521.20.57.336

Visit for more related articles at Global Media Journal

Abstract

Objective: from the perspective of data, this paper discusses the characteristics of the outbreak and ends of epidemic diseases and social communication, and provides a new idea for the research of epidemic diseases and social communication, which is important for understanding the characteristics of epidemic diseases and formulating more effective epidemic prevention measures.

Method: This paper starts from the perspective of data, based on the theory of complex networks, analyses the collected data related to influenza, measles and COVID-19, and draws on the epidemic transmission theory to study the characteristics of the spread and end of the epidemic from the perspective of data, and successively explores the hysteresis loop phenomenon The estimation method of news dissemination potential in social media and the influence of susceptibility and contact matrix on the spread and control of COVID-19.

Results/Conclusion: The results show that the outbreak process and the end process of epidemic transmission are asymmetric, and the area of hysteresis loop is paradoxically dependent on parameters in the state space and parameter space. A theoretical derivation method of effective reproduction number in public opinion communication is proposed. Using this method can help people judge the propagation potential of events and provide theoretical guidance for formulating effective control strategies. The numerical simulation results obtained through the SIR model prove that the changes in susceptibility and contact matrix have a great impact on the transmission of COVID-19, which is the main reason for the age and gender heterogeneity in cases. Our research shows that there are age and gender differences in the transmission of COVID-19, which is important to develop more effective epidemic prevention measures.

Keywords

Epidemics; Social Transmission; Hysteresis Loop; COVID-19; Susceptibility; Contact Matrix

Problem Statement

As a new interdisciplinary, complex network has aroused the common interest of experts in different fields such as physics, mathematics, and biology and computer science. The complex network theory has been applied to the research of epidemic, social communication, traffic flow and brain science. The research on epidemic and social communication has two main purposes: to suppress the outbreak of epidemic and accelerate the extinction. Scholars have used the theory of complex networks to study the spread of epidemics for more than 20 years, and have made fruitful research results. However, there are still many important issues to be studied and solved in scientific research, such as revealing the true spread characteristics of epidemic diseases, accurately predicting the spread trend of epidemic diseases, and proposing more effective control strategies. When studying epidemic and social transmission, scholars often use the method of extending the original model to explore new phenomena. Although this research method is reasonable, it is not conducive to revealing features beyond the traditional model, especially for some new diseases or situations that cannot be described by the traditional model [1, 2].

In this study, we adopt completely opposite research ideas. Before studying the model, we first collect and analyse data to find the topics to be studied. In the study of epidemic diseases, scholars mainly focus on the outbreak process of epidemic diseases, while ignoring the end stage of epidemic diseases. One of the consequences is that, in the face of the COVID-19 outbreak, because there is no responding theoretical support, governments cannot find effective control strategies. Considering that the research methods of social transmission and epidemic are similar, we studied the dynamic behavior of virus and information transmission on social networks in this paper. By analysing the data of influenza, measles and COVID-19, this paper discusses the characteristics of the outbreak and end of epidemic transmission, deduces the theoretical method of effective reproduction number in public opinion transmission, and further studies the impact of susceptibility on the transmission of COVID- 19 [3, 4].

Research design

Research method

Based on the complex network theory, this paper takes the spread and end characteristics of epidemic diseases as the research object, and carry out the following three works:

By analysing the data of influenza and measles, we can reveal the asymmetry between the outbreak process and the end process of the epidemic spread, and theoretically analyse the physical mechanism behind it from the perspective of the hysteresis loop to explain the paradox that the area of the hysteresis loop depends on parameters in the state space and parameter space [5-8].

Based on the epidemic spread theory, this paper intends to derive the theoretical method of effective regeneration number in public opinion communication, and verify the method with micro blog data. Specifically, the responding time series of the number of new participants in the daily topic discussion is obtained by analysing the forwarding data of different events on the micro blog platform, and the effective regeneration number is used to judge the spread potential of the epidemic or the message. The core of the derivation is as follows: According to Bayesian theorem, the time series of the number of new participants in daily topic discussion follows Poisson distribution, which is related to the distribution of generation time and effective regeneration number. By using Daley Kendall model to simulate the propagation process of messages and record all the propagation information of each node, we find that the time distribution generated in the public opinion model meets the negative binomial distribution. When we know the distribution of the time series and the generation time of the newly added topic, we can use the Markov chain Monte Carlo method to calculate the effective regeneration number [9, 10].

According to the collected data related to COVID-19, the impact of susceptibility on the transmission of COVID-19 was studied. Specifically, by analysing the confirmed case data of COVID-19 in Wuhan and Shanghai, calculate the probability of symptoms of individuals of different ages and genders, and combine the contact matrix of COVID-19 population before and after the COVID-19 outbreak, use the SIR model with age and gender structure to study the impact of changes in susceptibility and contact matrix on the transmission of COVID-19.

Burst and end characteristic hysteresis loop phenomenon

Epidemic transmission is one of the hottest topics in the field of complex network research, and has made remarkable achievements, including: infinitesimal threshold; Reaction diffusion model; Stream driven model; Time-varying network; Adaptive network, etc. One of the commonalities of these efforts is the infection rate during the spread of the epidemic. The change curve of infection density versus infection rate β I was a second-order phase transition [11, 12].

In research, we usually randomly select one or a small proportion of nodes as the infection seed, and then let the infection rate β increase from 0 to 1, and increase Δ β every time, And on each β value, take system of the starts to evolve from the same initial state until the system reaches steady state. So we can get the infection density βI. The bifurcation diagram of the change, so as to roughly determine the value of β_c By analysing the infection density when the infection rate value is near the threshold value βI. The change of I can determine the phase change type of the epidemic outbreak process [13].

Establishment of epidemic transmission model: Generally, nodes in the network can be divided into four types: susceptible, latent infected and recovered. The nodes in the network that can be infected but have not been infected are called vulnerable nodes; The node that has been infected but has not been diagnosed is called the latent node; The node with confirmed infection is called the infected node; The cured and immune node or the node that is removed from the network after death is called immune node. The susceptible node has a probability of being infected by the infected node and becoming a latent node. If the number of infected nodes around the susceptible node is kinf > 1, then the probability of being infected is 1-(1-β) kinf; Latent node has the probability of γ to become an infected node; The infected node has the probability of μ to become a recovery node. Commonly used, S, E, I, R and s, e, r represent the number and density of susceptible nodes, latent nodes, infected nodes and immune nodes respectively [14, 15].

Basic regeneration number Ro, effective regeneration number Rt, infection rate threshold βc. Average transmission time Ts and average generation time Tq are the most basic parameters in epidemiology. Introduce an infection in a network that is all susceptible nodes Node. The average number of susceptible nodes that can be infected by the infected node is called the basic regeneration number Ro. At the beginning of the epidemic, if Ro>1, the number of infected nodes increases. According to Ro=1, the threshold of infection rate can be calculated βc. Common Ro = 1 and β= βc to judge whether the epidemic can break out. The average number of susceptible nodes that can be infected by newly infected nodes at time t is called the effective regeneration number Rt at time Classic epidemic transmission models include SIS model, SIR model and SEIR model. This study will use SIR or SEIR model to establish the transmission model of COVID-19 [16-18].

Basically, other models are derived from the changes of these three models. In SIS model, there are only susceptible nodes and infected nodes in the network, and the nodes are evenly mixed. Expressed by s (t) and i (t) respectively:

When the system reaches steady state, di (t)/dt=ds (t)/dt=0.

In the SIR model, nodes are divided into susceptible nodes, infected nodes and immune nodes β Is infected, and the infected node μ The probability of is restored to the immune node, and the responding dynamic equations are as follows.

Analysis of the Delay Phenomenon of Epidemic Transmission on Complex Networks

By analysing influenza data in Hong Kong and measles data in New York and Baltimore, we found that the transmission process of epidemics can be divided into outbreak process and end process, and the two processes are asymmetric, forming a hysteresis loop. By making the system change the infection rate adiabatic before evolving to the steady state, we successfully reproduce the hysteresis loop in SIS model and SIRS model, and make it clear that the hysteresis loop is caused by the memory of the system before evolving to the steady state. In addition, we also studied the dependence of the area of the hysteresis loop on the parameters, and found a "bell shaped" hysteresis loop. Further analysis of the data shows that the hysteresis loop in the data is found in the state space, while the previous work is a hysteresis loop reproduced in the parameter space [19].

With this in mind, in this work, we directly study the characteristics of the hysteresis loop in the state space during the end of the epidemic. Using the same model, we successfully reproduce the hysteresis loop in the data in the state space, and find that the area of the hysteresis loop is completely opposite to the conclusion in the parameter space in terms of parameter dependence, which leads to a paradox. In the parameter space, when the infection rate increment is fixed, the larger the evolution time T, the smaller the area of hysteresis loop; When the evolution time is fixed, the larger the infection rate increment is, the larger the area of hysteresis loop is. But in the state space, when the infection rate increment is fixed, the larger the evolution time is, the larger the area of the hysteresis loop is; when the evolution time is fixed, the larger the infection rate increment is, the smaller the area of hysteresis loop is. Through theoretical analysis, we find that the calculation method of the area of different hysteresis loops in the two spaces is the cause of the paradox, and the paradox can be eliminated by parameter substitution and controlling the length of evolution time. Finally, we use mean field theory to prove the results of numerical simulation [20-22].

We find that the time series of epidemics is composed of outbreak peaks and background noise, and the spread process of epidemics can be divided into outbreak process and end process. The two processes are asymmetric, forming a hysteresis loop. By analysing the cold data in Hong Kong and the measles data in New York and Baltimore, we proved that the hysteresis loop characteristic in the data is universal. Figure 1 (a) shows the measles data in New York. We found that the outbreak peaks in the data are asymmetric. Randomly select an explosive peak from Figure 1 (a), mark it with a blue circle and the enlarged result is shown in Figure 1 (b).

By observing Figure 1 (d), we can find that the area of other peaks is similar except for No. 8 explosive peak. Looking at Figure 1 (e), we can find that the area of all outbreak peaks is greater than 0, which indicates that the hysteresis loop is a common phenomenon of epidemics. In addition, by comparing Figure 1 (d, e) (Figure 1).

We use this model to study the mechanism of hysteresis loops in state space. During the outbreak β Increase from 0 to βmax, each increase Δ β At the end of the process β from βmax decreases to 0, each time it decreases Δ β. After every time step of system evolution, the infection rate will change once β. The function expression of is as follows:

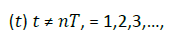
Where, "+" responds to the burst process and "-" responds to the end process. In addition, the initial state of the system in the next infection rate value will inherit the last state of the evolution of the previous infection rate value system, rather than resetting the system, starting from the same initial state. We use SIS model to simulate the spread of epidemic. In the SIS model, nodes are divided into susceptible nodes and infected nodes. The susceptible nodes will β Is infected, and the infected node will μ Under the probability of. When the number of infected nodes around the susceptible node k_ When inf>1, the probability of the susceptible node being infected by the infected node is

Calculation of message propagation potential on social media

We use the Delay Kendall model to simulate the message propagation process, and use the ABM method to record all the information of each node in the entire propagation process. Analysing the results of numerical simulation, we found that the distribution of generation time φ (t) satisfies the negative binomial distribution, and the average propagation time r (t) is highly related with the average generation time T (t). In this work, we propose a complete set of theoretical methods to identify the propagation potential of messages in social media. This theoretical method only requires the time series of the number of participants in the topic discussion every day, and other relevant parameters can be derived theoretically. The core of the theoretical method is as follows: according to Bayesian theorem, C (t) obeys Poisson distribution, which is related to the distribution of generation time φ (t) is related to the effective regeneration number R. Known C (t) and φ (t) then we can use the Markov Chain Monte Carlo method to calculate R. Finally, we apply this method to judge the propagation potential of different events on the micro blogging platform (Figure 2).

Figure 2 is a schematic diagram of the theoretical method. The first step is to input data, that is, the time series of the number of new participants in the discussion every day (t). The second step is the core of the whole method. We need to know the distribution of the generation time of the message. Figure 2(B) shows the shape of the distribution of generation time at two times selected from 2(A). Then, under the framework of Bayesian theory, MCMC method is used to estimate its effective regeneration number R t, that is, output data [23].

Influence of susceptibility and exposure mode changes on the transmission and control of COVID- 19

In this work, we use data from two sources. The first data was collected by the China Center for Disease Control and Prevention. This data statistics the daily summary data of COVID-19 diagnosed by laboratory in other regions of Hubei Province (except Wuhan for short) and provinces and cities outside Hubei Province (Hubei for short). As of February 25, 2020, the data recorded the gender and age information of each case. The second data source is quoted from reference, which records the age and gender information of confirmed cases of COVID-19 in Wuhan and outside Hubei Province. The data is up to March 16, 2020. Due to the problem of reporting rate, both data will lose some cases, so we compared the two data to verify the accuracy of the data, and the results are shown in Table 1. In Table 1, we use R to indicate susceptibility, that is, the risk of COVID-19 infection. The R in the follow-up results represents susceptibility (Table 1), (Figure 3).

Table 1. The consistency between official data reported by China CDC and personal record data.

From the references (J. T. Wu et al., 2020), we have obtained the contact matrix of the people in Wuhan and Shanghai before and after the outbreak of COVID-19. Figures 4 and 5 show the gender specific contact matrix.

Comparing Figure 4 (A, B) and (C, D), we can find that the average exposure times of men and women before the outbreak of COVID-19 can reach a maximum of 12, but the average exposure times after the outbreak are less than 1. By observing Figure 4 (A), we can know that the average exposure times of male age group 15-19 and age group 10-14 are the largest. Looking at Figure 4 (B), we can find the largest average number of contacts in female age is group 65+ and age group 55-59.

Comparing Figure 5 (A, B) and (C, D), we can find that the average contact times of men before the outbreak of COVID-19 can reach 14 times, the average contact times after the outbreak are less than 1 time, while the average contact times of women before the outbreak can reach 20 times, and the average contact times after the outbreak are about 2 times. By observing Figure 5 (A), we can know that the average exposure times of male age group 15-19 and age group 15-19 are the largest. Looking at Figure 5 (B), we can find that the average number of contacts of female age group 10-14 and age group 10-14 is the largest.

Figures 6 and 7 shows the average number of contacts between the people in Wuhan and Shanghai before and after the outbreak of COVID-19 among all age groups, that is, the average contact matrix (Figures 4-7).

In addition, we also analysed the proportion of male and female contacts in different age groups and the same age group in Wuhan and Shanghai. The results are shown in Figures 8 and 9. For Wuhan area, before the outbreak of COVID-19, the average contact times of men and women with the same age group first increased and then decreased with age, and the proportion of male and female age groups 10-14 and the same age group was the largest; After the outbreak of COVID-19, the average number of contacts with the same age group, both men and women, showed an overall increasing trend. The male age group 60-64 and the same age group had the largest proportion of contacts, while the female age group 65+ and the same age group had the largest proportion of contacts. For the Shanghai area, the proportion of male and female age groups 10 to 14 who contacted their peers was the largest before the outbreak of COVID-19; After the outbreak of COVID-19, the proportion of contact with peers showed an overall upward trend, with the largest proportion of men aged 60-64 and women aged 65+ (Figures 8 and 9).

Results of numerical simulation

Mechanism of the hysteresis loop

In the numerical simulation, we use a random network with the number of nodes N=10000 and the average degree k=6, and set μ= 0.2, 100-time steps of the system in both the burst process and the end process to study the mechanism of the hysteresis loop in the state space and the influence of parameters on the area of the hysteresis loop. The results are shown in Figure 10. In Figure 10 (a), we set T=1 to study Δ β. For the influence of the area of hysteresis loop, it can be found that the hysteresis loop can also appear in the state space using the same model, which shows that the memory effect before the system evolves to the steady state is also the reason for the hysteresis loop in the state space. In addition, we can find that when the evolution time T is fixed, Δ β = 0.001 responds to a large hysteresis loop area St. In Figure 10 (b), we set Δ β= 0.01 to study the influence of T on the area of hysteresis loop, in which the area of hysteresis loop Responding to T=5 is larger (Figure 10).

Next, we study the dependence of the area SΔt of the hysteresis loop in the state space on the parameters. The results are shown in Figure 10 (c, d). By observing Figure 10 (c), we can find that when the evolution time T is fixed, the infection rate increases by Δ β. The larger the hysteresis loop, the smaller the area SΔt. This indicates that the system has a threshold of Δ βc. When Δ β < Δ βc, the system will have hysteresis loop; When Δ β ≥Δ βc ,the system will not have hysteresis loop when the. The sub graph in Figure 11 (c) shows the area of hysteresis loop SΔt, and the infection rate increment, Δ β satisfy the power law relationship.

From Figure 10 (d), we can find that when the infection rate increases by Δ β When fixed, the larger the evolution time T is, the larger the area St of the hysteresis loop is. This indicates that the system has a threshold value Tc. When T<T, the system does not have a hysteresis loop; when T>Tc, the system will have a hysteresis loop. The sub graph in Fig. 10 (d) shows that the area of hysteresis loop, SΔt, and the evolution time, T, satisfy a power law relationship.

Figure 11 shows the relationship among the area SΔt, evolution time T and infection rate increment Δ β of hysteresis loop under three-dimensional figure, we get the same conclusion as Figure 10 (c, d). When the evolution time T is fixed, SΔt increases with Δ β Increasing and decreasing monotonously; when the infection rate increases by Δ β when fixed,SΔt increases monotonously with the increase of T (Figures 11 and 12).

Figure 12 shows that when SΔt takes different values, Δ β We can find that when the area of hysteresis loop is the same, Δ β There is a linear relationship between T and T. In order to keep SΔt unchanged, the larger Δ β Need to match a large evolution time.

Next, we compare the area of hysteresis loop with the infection rate increment Δ β in the two spaces β and evolution time T. Figure 13 (a-d) shows the responding results in the parameter space. sh represents the area enclosed by the hysteresis loop in the parameter space. In the parameter space, the infection rate increment Δ β When fixed, the larger the evolution time T is, the smaller the area Sn of hysteresis loop is; When the evolution time T is fixed, the larger the infection rate increment Δ β is, the larger the hysteresis loop area sh is. This conclusion is completely contrary to the conclusion in the state space, and there is a paradox in the dependence of the area of the hysteresis loop in the two spaces on the parameters (Figure 13).

In order to find out the cause of the paradox, we return to the definition of the area of the hysteresis loop in two spaces. Use pg and pc to express the infection density of the outbreak process and the end process respectively, then the expression of the area of the hysteresis loop in the state space is as follows:

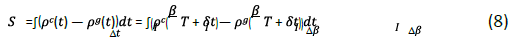
Among Represents the integer part of t/T, δt represents the fractional part of t/T, then δ the size of t is between [0, T). When δt changes between [0, T), the infection rate β Leave unchanged.

In the approximate case, we can use pg and pc .The average value of pg and pc between [0, T] replaces pg (t) and (t), the following relationship is obtained:

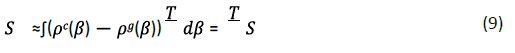
According to equation (4), we can find that the simple despondence between SΔt and sh is satisfied.

Relationship, we can put (β) convert to p(t), convert β to Δt.The result is shown in Figure 7.

We find that the curves in the parameter space are completely coincident with the curves in the state space after transformation, that is, the paradox mentioned above is caused by the different calculation methods of hysteresis loops in the two spaces, and the paradox can be eliminated by changing the parameters (Figure 14).

In Figure 14(a, b), although the total evolution time of the system is different, it is enough to complete the evolution of the whole hysteresis loop. Considering that the climate change in real life is impermanent, which can rain or clear suddenly, the responding system in the model does not have enough evolution time to complete the evolution of the whole hysteresis loop. We set the system to evolve 20 time steps in both the burst phase and the end phase, and the results are shown in Figure 8. When the total evolution time length is fixed, the larger the infection rate increment Δ β is, the larger the area SΔt and sh of the hysteresis loop is; the smaller the transient evolution time length T is,the larger the areas SΔt and sh of the hysteresis loop are. The conclusions are consistent with those in the parameter space, which shows that we can eliminate the paradox mentioned above by controlling the total evolution time length.

Numerical simulation results verification

We use mean field theory to verify the results of numerical simulation. For SIS model, infection density ρ R satisfies the following equation:

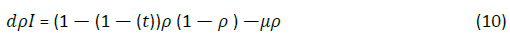
Represents the average value of infected neighbors around the node. During the entire evolution process, k; Over time. For the convenience of writing, we rewrite the above formula as follows:

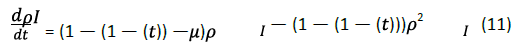
Next, we solve the functional expressions of infection rate density in the burst process and the end process respectively. For explosive processes, when nT<t<(n+1) T, β (t)= n Δβ,p_l(t) = pl(nT)

Substituting these two conditions into the above equation, we can get:

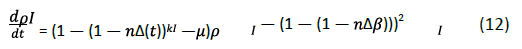
Divide both sides by p2, the following formula is obtained:

Then let t=nT and substitute the above equation to get:

According to equation 7 and 11, we can get the calculation formula of the area of the hysteresis loop in two cases:

Figure 16 shows the responding theoretical results. We can find that the simulation is very good according to the results of mean field theory and numerical results (Figures 15-17).

Next, we study the influence of network structure on hysteresis loop. We construct a scale-free network with the same node size and evenness as the random network. Figure 17 shows the area of the hysteresis loop in the scale-free network with respect to the infection rate increment Δ β and evolutionary time. Comparing Figure 10 and Figure 16, we find that SΔt the samedependency relationship with T, which proves that SΔt has the same dependency relationship with T and Δ β. Figure 18 shows the three-dimensional diagram of reliable relationship between the area of the hysteresis loop in the scale-free network SΔt and the infection rate increment Δ β, the dependence on evolution time T (Figure 18).

Conclusion and Enlightenment

In the first work, we focused on the end process of the epidemic, and found that the epidemic transmission process can be divided into the outbreak process and the end process. These two processes are asymmetric, forming a hysteresis loop. Through the research, we found that the memory effect before the system evolving to the steady state is the cause of the system hysteresis loop, and studied the dependence of the area of the hysteresis loop on the parameters in the parameter space. Considering that the hysteresis loop in the data is found in the state space, in this work, we directly studied the hysteresis loop in the state space, and found that the area of the hysteresis loop in the state space is related to the infection rate increment Δ β. Contrary to the time dependence of evolution and the conclusion in parameter space, this leads to a paradox. Through analysis, we find out the causes of the paradox and the methods to eliminate it. In addition, we also studied the influence of network structure, and found that the same conclusions can be obtained in scale-free networks as in random networks, which shows that the area of the hysteresis loop is robust to parameter dependence. We study hysteresis loops directly in state space. Using the same model as in the parameter space, we also reproduce the hysteresis loop in the data in the state space. In the state space, when the infection rate increases Δ β, the longer the evolutionary time is, the larger the area of the hysteresis loop is; When the evolutionary time T is fixed, the infection rate increases Δ β, the larger the hysteresis loop is, the smaller the area is. In the parameter space, when the infection rate increases Δ β until fixed, the larger the evolution time is, the smaller the hysteresis loop area is; when the evolutionary time T is fixed, the infection rate increases Δ β, the larger the hysteresis loop, the larger the area is. The area of the hysteresis loop in the two spaces depends on completely opposite parameters, which leads to a paradox. Through analysis, we found the cause of contradiction in the calculation formula of different hysteresis loop areas in the two spaces, and can change t=T through parameter transformation β⁄ Δ β, And the method of controlling the total evolutionary time length to eliminate the paradox. In addition, we also found that when the area of the hysteresis loop is unchanged, the infection rate increases Δ β And evolution time satisfy linear relationship. By using different network structures, we find that the area of the hysteresis loop is related to the infection rate increment Δ β and evolutionary time. Next, we will focus on the contribution of this work. In general, by analysing the data of influenza and measles, we further revealed the asymmetry between the outbreak process and the end process of epidemic transmission, theoretically analysed the physical mechanism behind it from the perspective of the hysteresis loop, and explained the paradox that the area of the hysteresis loop depends on the parameters in the state space and parameter space. It is hoped that the two work we have done can arouse scholars' attention to the process of the end of the epidemic and carry out relevant research. In this way, in the face of the outbreak of the epidemic, our work can provide theoretical guidance for the country to formulate effective strategies, so as to quickly eliminate the epidemic and reduce the damage caused by the epidemic.

In the second work, we studied the propagation of information, and found that the average propagation time of messages is highly related with the average generation time, and the distribution of the average generation time satisfies the negative binomial distribution. Under the framework of Bayesian theory, we propose a whole set of theoretical methods to estimate the effective basic number of regeneration of messages. The biggest advantage of this method is that it does not rely on the initial conditions and only needs some C (t) data. Any other parameters can be estimated by theoretical methods, and the accuracy of the estimation results is high. After obtaining the change curve of the effective regeneration number Rt of the event, we can judge the propagation potential of the event at different times according to Rt. In addition, we can predict its future propagation through machine learning, compare C (t) of different events to judge the propagation potential of other events, which can help people develop more effective control strategies. In general, our work provides a theoretical method for deriving the effective regeneration number in the public opinion model. Using this method can help people judge the propagation potential of events and provide theoretical guidance for formulating effective control strategies.

In the third work, by analyzing the age and gender characteristics of early COVID-19 cases in

Wuhan and Shanghai, and estimating the relative risk related to susceptibility, we found that the

Intervention measures implemented in these two regions had a control effect on the spread o

COVID-19. In Wuhan and Shanghai, the number of confirmed cases of COVID-19 increases with

Age. The median age of the confirmed cases in Wuhan, Shanghai and other places outside Hubei

Province, whether male or female, did not change significantly over time. The impact of

Population mobility (input cases) is mainly reflected in the age groups and 65+. It has nothing to do with gender. Specifically, among men, the changes in age groups and 65+ are the largest, while among women, the changes in age groups. And 65+ are the largest. When fitting the total number of COVID-19 infections in various age groups in Wuhan and Shanghai, we found that the age and gender differences in the data could not be fitted using the same R, but the age and gender differences in the data could be fitted using the age and gender related susceptibility R. In general, based on the collected data related to COVID-19, we studied the impact of susceptibility on the transmission of COVID-19 in the third work. Our research has improved the understanding of the spread of COVID-19, which is of great significance for developing more effective intervention measures.

References

1. X Li M, Geng Y, Peng L, Meng S (2020) Molecular immune pathogenesis and diagnosis of COVID-19. Pharm Anal 10: 102-108.

Indexed at, Google Scholar, Crossref

2. Prompetchara E, Ketloy C, Palaga T (2020) Immune responses in COVID-19 and potential vaccines: Lessons learned from SARS and MERS epidemic. Asian Pac J Allergy Immunol 38: 1-9.

Indexed at, Google Scholar

3. Qin C (2020) Deregulation of Immune Response in Patients with Coronavirus 2019 (COVID-19) in Wuhan, China. Clin Infect Dis 71: 762-768.

Indexed at, Google Scholar, Crossref

4. Viner RM (2020) Susceptibility to and transmission of COVID-19 amongst children and adolescents compared with adults: a systematic review and meta-analysis medRxiv.

Google Scholar, Crossref

5. Davies NG (2020) Age-dependent effects in the transmission and control of COVID-19 epidemics. Nature Medicine 26: 1205-1211.

Indexed at, Google Scholar

6. Nikolich-Zugich J (2020) SARS-CoV-2 and COVID-19 in older adults: what we may expect regarding pathogenesis, immune responses, and outcomes. Geoscience 42: 505-514.

Indexed at, Google Scholar

7. Verity R (2020) Estimates of the severity of coronavirus disease 2019: a model-based analysis. The Lancet Inf Dis 20: 669-677.

Indexed at, Google Scholar, Crossref

8. Maier BF, Brockmann D (2020) Effective containment explains sub exponential growth in recent confirmed COVID-19 cases in China. Science 368: 742.

Crossref

9. Rader B (2020) Crowding and the epidemic intensity of COVID-19 transmission. MedRxiv, 20064980.

Indexed at, Google Scholar, Crossref

10. Wu JT (2020) Estimating clinical severity of COVID-19 from the transmission dynamics in Wuhan, China. Nat Med 26: 506-510.

Indexed at, Google Scholar, Crossref

11. Wu JT, Leung K, Leung GM (2020) now casting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modeling study. The Lancet 395: 689-697.

Indexed at, Google Scholar, Crossref

12. Chinazzi M (2020) the effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 368-395.

Indexed at, Google Scholar, Crossref

13. Kraemer MUG (2020) the effect of human mobility and control measures on the COVID-19 epidemic in China. Science 368-493.

Indexed at, Google Scholar, Crossref

14. Pan A (2020) Association of Public Health Interventions With the Epidemiology of the COVID- 19 Outbreak in Wuhan, China. JAMA 323: 1915-1923.

Google Scholar, Crossref

15. Zhang J (2020) Changes in contact patterns shape the dynamics of the COVID-19 outbreak in China. Science 368: 1481.

Google Scholar, Crossref

16. Zhang J (2020) Evolving epidemiology and transmission dynamics of coronavirus disease 2019 outside Hubei province, China: a descriptive and modeling study. The Lancet Infectious Dise20: 793-802.

Indexed at, Google Scholar, Crossref

17. Gomes MGM (2020) Individual variation in susceptibility or exposure to SARS-CoV-2 lowers the herd immunity threshold. Med Rxiv.

Google Scholar

18. Weitz JS (2020) Modeling shield immunity to reduce COVID-19 epidemic spread. Nature Medicine 26: 849-854.

Google Scholar

19. Zhai Z M (2020) State-by-State prediction of likely COVID-19 scenarios in the United States and assessment of the role of testing and control measures. Med Rxiv.

Google Scholar, Crossref

20. Long YS (2020) Quantitative assessment of the role of undocumented infection in the 2019 novel coronavirus (COVID-19) pandemic.

Google Scholar, Crossref

21. Zhai ZM, Long YS, Tang M, Liu Z (2020) When did COVID-19 start? Optimal inference of time ZERO.

Google Scholar

22. Liu QH (2018) Measurability of the epidemic reproduction number in data-driven contact networks. Proceedings of the National Academy of Sciences 115: 12680.

Google Scholar, Crossref

23. Li A, Cornelius SP, Liu YY, Wang L Barabasi (2017) The fundamental advantages of temporal networks. Science 358: 1042.

Indexed at, Google Scholar, Crossref